Random Coprimes and Pi
October 10, 2016
I've always enjoyed doing
computer simulations. While I enjoy doing
math, simulations are a way to get useful information without too much
mental exercise. If you're
lucky, scratching away with
pencil on
paper will get you an
analytical solution for your problem, but often the
approximate results of a simulation will quickly get you the information you need to move forward on a project.
One feature of most simulations is
random numbers; and, as we know,
computers can
generate pseudorandom numbers that look good to the casual observer, but they're not good enough for
cryptography and many simulations. One problem is that generators have a
cycle length, and the pseudorandom sequence starts to repeat when you demand too many numbers. Another is that the random distribution is not quite
uniform.
Dice are associated with randomness.
A Google image search shows many math-themed dice.
(Via Wikimedia Commons.)
The
programming languages of today have fairly good
random number generating functions, and I use the random number function,
rand(), in the
C language for simple simulations with good results. Seasoned simulators would never use such built-in generators, since better generators are easy to program. Is there a way to test such generators?
There are actually quite a few different
statistical tests for randomness, some involving dice throws, and more exotic ones that simulate
monkeys on typewriters.
American mathematician and
computer scientist,
George Marsaglia (1924-2011), collected many of these together into a series of tests called
Diehard.[1] Better random number generators give better Diehard scores.
One popular and
efficient random number generator that scores well in Diehard is the
Mersenne twister.[2-3] This generator gets its name from the fact that its period is a
Mersenne prime. Mersenne primes are
prime numbers of the form
2n - 1, but such primes are rare. There are just 45 Mersenne primes in the first 2,270,720 primes. The period of the commonly used Mersenne Twister is
219937-1, which is the 24th Mersenne prime.

Marin_Mersenne (1588-1648).
Mersenne was friends with Descartes, and also friends with the father of Blaise Pascal, and he notably applied mathematics to acoustics.
His Mersenne's laws describe the oscillation frequency of stretched stringss.
(Wikimedia Commons image, modified for artistic effect.)
Source code for the Mersenne Twister is available at many places on the
Internet.[3] My implementation, in the C programming language, can be found
here. This demonstration program also includes a simple test of this generator's uniformity, as shown in the graph, below.
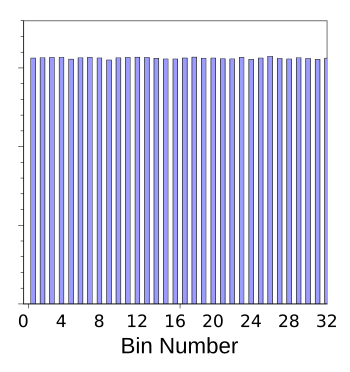
Portion of a histogram of ten million Mersenne twister pseudorandom numbers as output from the author's program.
(Graphed using Gnumeric.)
My interest in simulation was recently excited by a
paper on
arXiv by
Sergei Abramovich of
St.Petersburg University and
Yakov Yu. Nikitin of the
State University of New York at Potsdam.[4] This paper reviewed the simple problem of
calculating the
probability P of the
coprimality of two
natural numbers chosen at random. The analytical solution, found by a couple of
teenagers, was published in a short, one page note.[5]
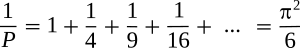
Abramovich and Nikitin write that this probability is found to be the same as the probability of a
fraction formed from random natural numbers being
irreducible; that is, the
numerator and
denominator are
coprime, and their
greatest common divisor is 1. What a perfect setup for a simulation to obtain a value for
pi - random numbers and a simple equation that gives pi as
√(6/P).
My simulation program can be found
here, with the results graphed below. I must admit that the program has not been carefully optimized, but it does use the Mersenne Twister as a random number generator.
Archimedes (c. 287 BC - c. 212 BC) calculated that pi is between 3.1408 and 3.1429. More than two
millennia later, I get the same
precision by this simulation. At least the exercise was good programming practice.
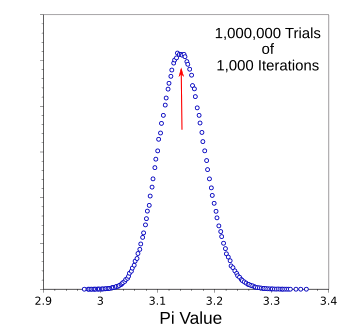
Histogram of values of pi obtained using the random coprime method.
The double loop of the simulation program gives a billion tests of coprimality.
(Graphed using Gnumeric from the data produced by the author's program.)
![]()
References:
- Robert G. Brown, Dirk Eddelbuettel, and David Bauer, "Dieharder: A Random Number Test Suite, Version 3.31.1," Duke University Web Site.
- M. Matsumoto and T. Nishimura, "Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator", ACM Transactions on Modeling and Computer Simulation, vol. 8, no. 1 (January, 1998), pp 3-30, doi:10.1145/272991.272995. A PDF copy can be found here.
- Takuji Nishimura, "A C-program for MT19937: Integer version," April 6, 1998.
- Sergei Abramovich and Yakov Yu. Nikitin, "On the probability of co-primality of two natural numbers chosen at random (Who was the first to pose and solve this problem?)," arXiv, August 18, 2016.
- A. D. Abrams and M.T. Paris, "The probability that (a, b) = 1," The College Mathematics Journal, vol. 23 (1992) p.47. (PDF file).
- Vassilios Hombas, "What's the probability of a rational ratio being irreducible?" International Journal of Mathematical Education in Science and Technology, vol. 44, no. 3 (2013), pp.408-410, doi.org/10.1080/0020739X.2012.703332.
Permanent Link to this article
Linked Keywords: Computer simulation; mathematics; math; thought; mental exercise; luck; lucky; pencil; paper; closed-form expression; analytical solution; approximation; approximate; random number; computer; pseudorandom number generator; cryptography; cycle detection; cycle length; uniform distribution; dice; randomness; Google image search; Wikimedia Commons; programming language; random number generation; random number generating function; C language; statistics; statistical; infinite monkey theorem; monkeys on typewriters; American; mathematician; computer science; computer scientist; George Marsaglia (1924-2011); Diehard tests; efficiency; efficient; Mersenne twister; Mersenne prime; prime numbers; Marin Mersenne (1588-1648); Descartes; father; Blaise Pascal; acoustics; Mersenne's laws; oscillation; frequency; fiber; string; source code; Internet; histogram; pseudorandom number; Gnumeric; academic publishing; paper; arXiv; Sergei Abramovich; St.Petersburg University; Yakov Yu. Nikitin; State University of New York at Potsdam; calculation; calculating; probability; coprime integers; coprimality; natural number; adolescence; teenager; fraction; irreducibility; irreducible; numerator; denominator; greatest common divisor; pi; Archimedes (c. 287 BC - c. 212 BC); millennium; millennia; precision; control flow; loop; double loop.