| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
The Proton Size Problem
November 3, 2016
It's easy to measure the
diameter of a
billiard ball to great
accuracy, but not that easy to measure the diameter of a
tennis ball. A tennis ball is
fuzzy, so it's hard to say where a tennis ball ends and the rest of the
universe begins. The same is true of the
subatomic particles, which, because of their
quantum nature, exist as fuzzy blobs. The
electron is an interesting case. While
experiments show that it is a "
point particle" with no diameter, we must conclude by
Heisenberg's uncertainty principle that it does occupy a nonzero
volume.
Werner Heisenberg (right), alongside Wolfgang Pauli, at the 1927 Solvay Conference.
(Photo by Benjamin Couprie, Institut International de Physique de Solvay, via Wikimedia Commons.)
While
protons act as if they are
charged spheres, the edge of the sphere is not sharply defined. The proton charge radius is therefore taken as a root-mean-squared value. There have been many measurements of this charge radius, and the accepted value is 0.8751 femtometers (fm, 1015 meter) with an uncertainty of about 0.7%.[1]
It's not known why a proton should have a particular charge radius, let alone the particular value that we measure. Also, the proton has a magnetic moment, acting as if it were a spinning ball of charge.
Otto Stern discovered the large magnetic moment of the proton, and he was awarded the 1943
Nobel Prize in Physics for this discovery.
Today, we know that the proton is a
composite particle composed of three
quarks, two
up quarks of electric charge +2/3 e and
spin 1/2 ↑, and one
down quark of electric charge -1/3 e and spin 1/2 ↓. Adding the charges and spins of these gives us the values that we observe for the proton.
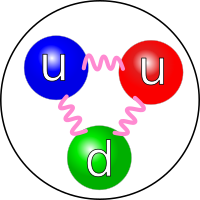
Quark structure of the proton.
The three quarks (two up and one down) are held together by appropriately named gluons.
(Image by Arpad Horvath, modified, via Wikimedia Commons.)
As I wrote in two previous articles (
Fat Protons, July 12, 2010, and Proton Size Problem, March 20, 2013), proton size measurements based on
hydrogen atoms in which
muon replace electrons have yielded a significantly smaller charge radius than previous measurements, giving rise to what's now termed the
proton radius puzzle.[2-4]
When a hydrogen atom is constructed from a muon and a proton, the proton appears to have a slightly smaller radius than that of a normal hydrogen atom of an electron
orbiting a proton. Although muons are 207 times heavier than electrons, all their other properties are identical, and theory predicts that the proton shouldn't behave differently.
ArXiv lists 61
papers containing "proton radius" in their title from 2010 to the present.
Muonic hydrogen provides a better system than electonic hydrogen for measurement of the proton charge radius, since the higher
mass muon is in a nearer orbit of the proton than an electron. These measurements have been based on pulsed laser spectroscopy of the Lamb shift of the muonic energy levels. The Lamb shift, named after
Nobel Physics Laureate, Willis Lamb, is the small difference in energy between the
2S
1/2 and
2P
1/2 electron energy levels.
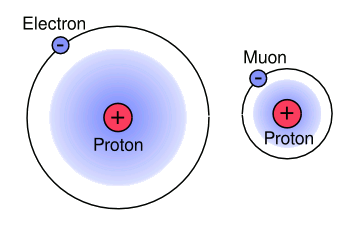
The Bohr models of hydrogen and muonic hydrogen drawn to scale.
(Illustration by the author using Inkscape.)
This is a difficult experiment, since muons have a
mean lifetime of just 2.197
microseconds. In this short time span, you need to create muonic hydrogen and measure the Lamb shift. Fortunately, the experimental teams have been able to create a few hundred muons each second, and a fraction of these replaced electrons in hydrogen gas.
Earlier this year, the same
research group that made the original discovery of the proton size problem conducted further experiments using muons with
deuterium nuclei, which are protons combined with a
neutron, and muons.[5-6] They found a proton radius several
standard deviations smaller than that of normal, electron deuterium. These repeated
confirmatory measurements show that, aside from some unknown experimental or
theoretical error, there might be some new
physics to be discovered, such as a previously unknown
fundamental force acting between muons and protons, but not between electrons and protons.[5-6]
Some new physics might explain the
anomalous magnetic dipole moment of the muon.[6] The lead
principal investigator on these experiments,
Randolf Pohl of the Max Planck Institute of Quantum Optics (Garching, Germany) is more cautious.[6] The proton size
calculation requires a value of the
Rydberg constant, which is supposedly known to great accuracy (10 973 731.568 508 m
-1).[7] Pohl thinks that the problem might be in this constant.[6]
As typical in the
sciences, works continues to unravel the true story. Another team is attempting a measurement that doesn't require the Rydberg constant, and Pohl's group plans to examine muonic
helium, a muonic atom with two protons.[6]
References:
- NIST, "CODATA Value: proton rms charge radius".
- Randolf Pohl, et al., "The size of the proton," Nature, vol. 466, no. 7303 (July 8, 2010), pp. 213-216.
- Aldo Antognini, et al. "Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen," Science, vol. 339 no. 6118 (January 25, 2013), pp. 417-420.
- Helen S. Margolis, "How Big Is the Proton?" Science, vol. 339 no. 6118 (January 25, 2013), pp. 405-406.
- Randolf Pohl, et al., "Laser spectroscopy of muonic deuterium, Science, vol. 353 no. 6300 (August 12, 2016), pp. 669-673, DOI: 10.1126/science.aaf2468.
- Natalie Wolchover, "New Measurement Deepens Proton Puzzle," Quanta Magazine, August 11, 2016.
- NIST, "CODATA Value: Rydberg constant".
Permanent Link to this article
Linked Keywords: Diameter; billiard ball; accuracy; tennis ball; fuzzy; universe; subatomic particle; quantum mechanics; quantum nature; electron; experiment; point particle; Heisenberg's uncertainty principle; volume; Werner Heisenberg; Wolfgang Pauli; Solvay Conference; Wikimedia Commons; proton; electric charge; charged; sphere; charge radius; root-mean-square; femtometer; proton magnetic moment; Otto Stern; Nobel Prize in Physics; composite particle; quark; up quark; spin; down quark; gluon; hydrogen atom; muon; proton radius puzzle; atomic orbital; orbiting; ArXiv; scientific literature; paper; mass; laser; spectroscopy; Lamb shift; energy level; Nobel Physics Laureate; Willis Lamb; energy; Bohr model; hydrogen atom; muon; muonic; Inkscape; exponential decay; mean lifetime; microsecond; hydrogen gas; research; deuterium; atomic nucleus; nuclei; neutron; standard deviation; reproducibility; confirmatory measurement; theory; theoretical; physics; fundamental interaction; fundamental force; anomalous magnetic dipole moment of the muon; principal investigator; Randolf Pohl; calculation; Rydberg constant; science; helium.