Particle Clumping
July 9, 2014
Since our earliest days, each of us has been concerned with the common
human activities of packing and filling. As
children, we needed to pack our
toys in our toy
chest and our
clothes in our
dresser drawers and
closet. We needed to fill our
bowl with
breakfast cereal without its overflowing, and the same for
cups of
milk. Not surprisingly, there's a lot of
science behind the optimal packing and filling of regularly- and irregularly-shaped items.
As I wrote in a
previous article (Packing and Filling, May 17, 2012) the optimal packing of
circle in a
plane occurs when their
centers are on an
hexagonal lattice. This packing gives an
areal density of (π/2√3) = 0.9069 (see figure).
Carl Friedrich Gauss proved that this packing was optimum for a lattice arrangement, and
László Fejes Tóth showed that this is the optimal packing, lattice or otherwise.[1]

Lattice packing of pennies in a plane.
(Base image of a US penny, via Wikimedia Commons.)
Circles, of course, are an easy target, so it's more interesting to extend packing to other shapes in
two dimensions, and to shapes in
three dimensions, trying to determine what their maximum
areal density and
volume density might be.
Computers are a big help in finding interesting
phenomena, as the following figure demonstrates. This
random packing of
isosceles triangles was done using a variant of the
Lubachevsky-Stillinger algorithm.

Random packing of isosceles triangles in a plane using a variant of the Lubachevsky-Stillinger algorithm.
(Illustration by L. Salgo, via Wikimedia Commons.)
In this example, as in many computer
mapping on the
plane, the
boundaries were wrapped; that is, triangles stepping over the right edge stepped into the left edge. The same was true for the top and bottom edges. The areal packing density of the triangles in the figure is 0.8776.
As I discussed in an
earlier article (Packing, November 30, 2010), jumping up one
dimension to go from packing
circles in a plane to
spheres in a
volume makes the
mathematics much more difficult. The one obvious candidate for the densest
packing of identical spheres is the
cannonball stacking used also by
greengrocers when they stack
fruit. This
close-packing arrangement is shown in the figure.
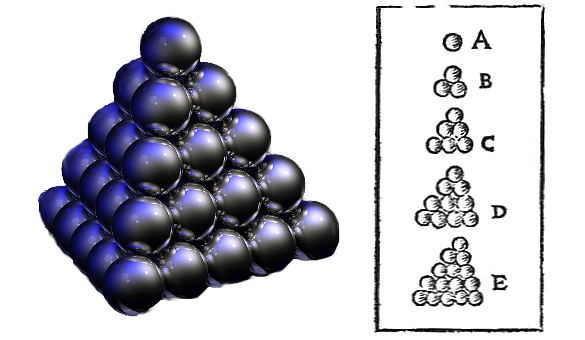
The well-known cannonball (close-packing) arrangement of spheres (right), along with the illustration that Johannes Kepler (1571-1630) used when making the conjecture that this is the densest possible arrangement. (Left image by "Greg L," and right image from Johannes Kepler's 1611 Strena Seu de Nive Sexangula, both images via Wikimedia Commons.)
Johannes Kepler (1571-1630) conjectured that this arrangement of spheres, whose volume density is π/(3√2) ≈ 0.74048, has the highest possible density, and this was proved for lattice arrangements by
Carl Friedrich Gauss (1777-1855). Note that stacking cannonballs on an
equilateral triangle base and a
square base gives the same packing, just with a different
spatial orientation.
Proving that this packing was the densest packing for all sphere arrangements, lattice or otherwise, was not accomplished for quite some time. Finally, in 1998,
Thomas Hales produced a "proof" which is much like the "proof" for the
four color conjecture. He used
computer programs to examine every possible case of sphere packing.[2]
If we're randomly packing spheres, the packing density comes in at 64%, which is quite a bit less than the 74% for close-packed lattice packing. In 2004,
Princeton University physicist,
Paul Chaikin (now at
New York University), and chemist,
Salvatore Torquato, found that random packing of
oblate spheroids can be larger.
M&M candy, for example, will randomly pack at 68%, while their lattice packing is about the same.[3-4]
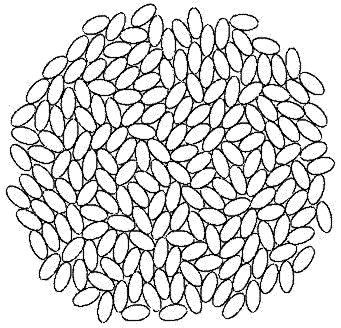
Monte Carlo simulation of packing of hard ellipses.
(image from the ChaikinLab Condensed Matter Physics Laboratory at New York University.)
Their
computer simulations found that a random stacking of
ellipsoids, which are closer in shape to a sphere than the
lenticular M&Ms, actually has a larger density than the close-packed lattice packing of spheres. Further work by Torquato [5-12] showed that the densest packings of
tetrahedra,
icosahedra,
dodecahedra, and
octahedra were 0.823, 0.836, 0.904, and 0.947, respectively. This is an interesting result, since the dodecahedra and icosahedra approximate a sphere to a high degree but pack much better.
Physicists use "
spherical cow"
models whenever possible, and it's easy to convince yourself that
natural particles will aggregate in a manner similar to the packings described above. One important such aggregate, since it's implicated in
global warming, is
atmospheric soot, which is composed of round particles of
carbon in a size range of about 10-20
nanometers.
Scientists from the
National Institute of Standards and Technology (NIST,
Gaithersburg, Maryland) and the
University of Maryland (College Park, Maryland) have measured the volume density of such weakly compacted aggregated materials, and they've found that it has a
scale invariant value of about 0.36 over many
orders of magnitude.[13-15]
Particle aggregates aren't limited to just atmospheric soot. They exist in
interstellar dust clouds from which
planets and
comets are formed, and in
microscale powdered pharmaceuticals.[13] Small aggregates grow into larger ones through compaction at low
compression, so the size of aggregates covers ten orders of magnitude, from soot to comets.[13] What the research team has found is that the packing of aggregates is remarkably independent of the aggregating
forces, the aggregation mechanism, and the
initial conditions.[13]
After making measurements on soot particles, getting the volume density of 0.36, and convincing themselves that this was the correct value (they obtained 0.36 ± 0.02), the team decided to do some confirmatory
experiments. They enlisted the help of a
high school and a
college intern (see photo), who
glued thousands of random combinations of spheres in clumps of 1-12 spheres, filled various sized
containers with these assemblies, and measured their volume fraction.[13]

Jessica Young, a high school student and an intern at NIST, doing a packing experiment.
Young's work aided NIST research on how rigid aggregates tend to clump together at roughly the same density regardless of scale.
(Image: Baum/NIST.)
The experiments proved that their
hypothesis, that 0.36 is the most likely value for the packing density of an aggregate, was correct. This value obtains also for fine, compacted
silica, as used in the manufacture of
ceramics, and for pharmaceutical powders made from "microscale random aggregates." Measurements by
NASA show that comet density is in the range of 0.2-0.4.[15]
References:
- Weisstein, Eric W. "Circle Packing." From MathWorld--A Wolfram Web Resource.
- Weisstein, Eric W. "Kepler Conjecture." From MathWorld--A Wolfram Web Resource.
- Steven Schultz, "Sweet science: Common candies yield physics discovery," Princeton University Press Release, February 12, 2004.
- Aleksandar Donev, Ibrahim Cisse, David Sachs, Evan A. Variano, Frank H. Stillinger, Robert Connelly, Salvatore Torquato and P. M. Chaikin, "Improving the Density of Jammed Disordered Packings Using Ellipsoids," Science, vol. 303, no. 5660 (February 13, 2004), pp. 990-993.
- Aleksandar Donev, Frank H. Stillinger, P. M. Chaikin and Salvatore Torquato, "Superdense Crystal Packings of Ellipsoids," arXiv Preprint Server, March 10, 2004.
- S. Torquato, "Reformulation of the Covering and Quantizer Problems as Ground States of Interacting Particles," arXiv Preprint Server, September 8, 2010.
- Salvatore Torquato and Frank H. Stillinger, "Jammed Hard-Particle Packings: From Kepler to Bernal and Beyond," arXiv Preprint Server, August 17, 2010.
- S. Torquato and Y. Jiao, "Exact Constructions of a Family of Dense Periodic Packings of Tetrahedra," arXiv Preprint Server, April 30, 2010.
- Y. Jiao, F. H. Stillinger and S. Torquato, "Novel Features Arising in the Maximally Random Jammed Packings of Superballs," arXiv Preprint Server, January 4, 2010.
- S. Torquato and Y. Jiao, "Dense Packings of Polyhedra: Platonic and Archimedean Solids," arXiv Preprint Server, September 9, 2009.
- S. Torquato and Y. Jiao, "Dense Packings of the Platonic and Archimedean Solids," arXiv Preprint Server, August 27, 2009.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, "Is Random Close Packing of Spheres Well Defined?," arXiv Preprint Server, March 25, 2000.
- Christopher D. Zangmeister, James G. Radney, Lance T. Dockery, Jessica T. Young, Xiaofei Ma, Rian You and Michael R. Zachariah, "Packing density of rigid aggregates is independent of scale," Proc. Natl. Acad. Sci. Early Edition, June 9, 2014, doi:10.1073/pnas.1403768111.
- Supporting information for ref. 13 (PDF File).
- Michael Baum, "Snowballs to Soot: The Clumping Density of Many Things Seems to Be a Standard," NIST Tech Beat, June 10, 2014.
Permanent Link to this article
Linked Keywords: Human; child; children; toy; chest; clothing; clothes; lowboy; dresser; drawer; closet; bowl; breakfast cereal; cup; milk; science; circle; plane; center; hexagonal lattice; areal density; Carl Friedrich Gauss; mathematical proof; László Fejes Tóth; penny; pennies; Wikimedia Commons; two-dimensional space; two dimensions; three dimensions; displacement; volume density; computer; phenomenon; phenomena; randomness; random; isosceles triangle; Lubachevsky-Stillinger algorithm; plane; mapping; border; boundary; dimension; sphere; volume; mathematics; sphere packing; packing of identical spheres; round shot; cannonball; greengrocer; fruit; close-packing of equal spheres; Johannes Kepler (1571-1630); conjecture; Carl Friedrich Gauss (1777-1855); equilateral triangle; square; spatial orientation; Thomas Callister Hales; four color theorem; four color conjecture; computer program; Princeton University; Paul Chaikin; New York University; Salvatore Torquato; oblate spheroid; M&M candy; Monte Carlo simulation; ellipse; ChaikinLab Condensed Matter Physics Laboratory; computer simulation; ellipsoid; lenticular; tetrahedron; tetrahedra; icosahedron; icosahedra; dodecahedron; dodecahedra; octahedron; octahedra; physicist; spherical cow; scientific modelling; model; nature; natural; global warming; atmosphere of Earth; atmospheric; soot; carbon; nanometer; scientist; National Institute of Standards and Technology; Gaithersburg, Maryland; University of Maryland (College Park, Maryland); scale invariance; scale invariant; order of magnitude; cosmic dust; interstellar dust clouds; planet; comet; micrometer; microscale; powder; pharmaceutical drug; pharmaceutical; compression; force; initial condition; experiment; high school; college; internship; intern; adhesive; glue; glassware; container; hypothesis; silicon dioxide; silica; ceramic; NASA.