| Tikalon Blog is now in archive mode.
An easily printed and saved version of this article, and a link
to a directory of all articles, can be found below: |
|
This article |
| Directory of all articles |
Parallax and Stellar Aberration
August 29, 2012
I was a
Boy Scout when I was in
sixth grade. The
Boy Scouts of America has recently been
an object of criticism, but in those days it was all fun. I learned how to make
fire using
flint and
steel, and I was awarded a few
merit badges.
After a while, my interests switched to
other areas; so, I dropped out of scouting, but not without learning that
moss grows on the
north side of a
tree. Now, if only my house were always north of where I was. There is one person for whom that's possible (Hint: He wears a read suit, he has a white beard, and he
husbands reindeer).
One amazing thing that I learned as a Boy Scout was how to measure great distances without
pacing them out. The technique was especially useful for measuring things that couldn't be paced, such as the width of
rivers. This was an application of
geometry before the subject was introduced in
elementary school.
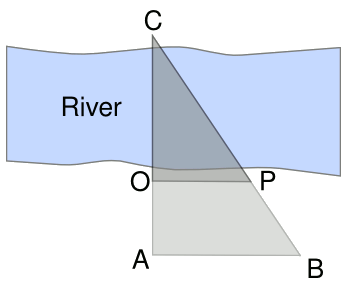
Distance measurement of the width of a river using similar triangles.
This method should be readily apparent to all geometers, but it's explained in the text.
(Figure rendered by the author using Inkscape)
The figure above shows the method for finding the width of a river. All that's required is a reference object, such as a tree, on the opposite side of the river, and some handy rocks to mark some points on your side of the river. You just pace the lines, OA and AB, walk the line BP, and pace the line, PO. Simple
algebra will give you the river width, OC, knowing that
triangles ABC and OPC are similar.
Later, in
high school physics, we did the same thing on the roof of our school. I doubt that today's students would be allowed to do the same thing, since there was no
guard railing around the roof.
This geometrical method is good on
Earth, but when you look upwards, towards the stars, you need to use
trigonometry, instead. The
ancient Greeks were able to measure the distance to the
Moon by noting its shift in angular position, its
parallax, when it was observed at one edge of the Earth, or the other. You don't need to be at two places at once. You just wait for the
Earth's rotation to carry you around from Moon-rise to Moon-set, resulting in a
diurnal parallax (see figure). The Moon does move over the course of those twelve hours, so a correction needs to be applied to get the proper distance. Of course, to the ancients, it wasn't the Earth that rotated; rather, the fixed stars revolved about the Earth.
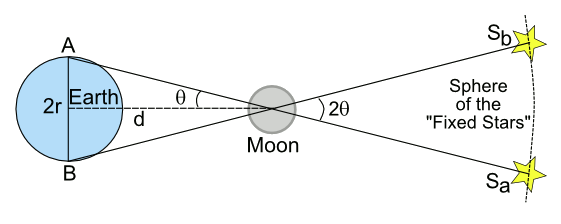
Finding the distance to the Moon. In ancient astronomy, it was all about the "fixed stars," those stars that never changed position, since they were affixed to a distant celestial sphere. Figure rendered by the author using Inkscape)
Todd Timberlake of
Berry College (Mount Berry, Georgia) has published a paper reviewing the history of parallax in
astrometry on the
arXiv Preprint Server.[1] Early
astronomers weren't too concerned with the fact that parallax of the stars wasn't observed, since their
geocentric model of the
universe put the Earth at its center. The stars were just too distant for their parallax to be seen from opposite sides of the Earth.
All this changed when the
Copernicus introduced his
heliocentric system. It was now apparent that the parallax of stars could be measured across the much wider breadth of the
Earth's orbit. Surprise! No parallax was found. Were the stars that distant; or, perhaps, was Copernicus wrong? When faced with a challenging measurement,
scientists roll up their sleeves and get to work refining their
instrumentation.
It took two
centuries before any parallax was found.
Friedrich Bessel, of the famous
Bessel functions, detected the parallax of the star,
61 Cygni, in 1838. The star, 61 Cygni, is 11.41
light years from Earth, a small figure by cosmic standards, but this distance corresponds to a parallax of just 286
milliarcseconds, One interesting side-effect of this search was the earlier discovery of another astronomical phenomenon,
stellar aberration.
The finite
speed of light (299,792,458
m/sec), combined with the
speed of the Earth along its orbit (on average, 29,780 m/s), leads to a shift in stellar position because the Earth could be moving traversely with respect to a star's light signal. The ratio of these speeds is just 0.01%, but the effect can be detected.
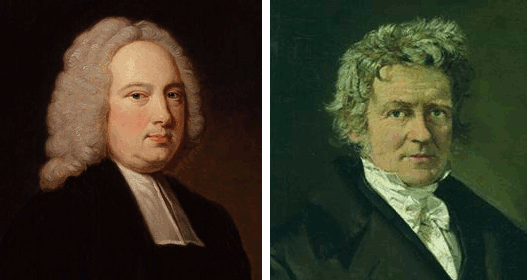
James Bradley (1693 - 1762, left) in a portrait by Thomas Hudson (1701-1779), from the National Portrait Gallery, London; and Friedrich Wilhelm Bessel (1784 - 1846) in a portrait by Christian Albrecht Jensen (1792–1870), from the Ny Carlsberg Glyptotek. Left image and Right image, via Wikimedia Commons)
This stellar aberration was discovered in 1725 by
James Bradley, who was the third
Astronomer Royal. Stellar aberration was detected long before stellar parallax, since its maximum value is about twenty
arcseconds, or nearly a hundred times greater than the parallax of 61 Cygni.
I close with the colorful first sentence of "An Attempt to Prove the Motion of the Earth by Observations," by
Robert Hooke.[2] Hooke attempted a parallax observation of
gamma Draconis in 1669. The detection of this parallax was not possible, since gamma-Draconis is at 154.3 light year's distance, and it has a parallax of only 21 milliarcseconds.
"Wether the Earth move or stand still hath been a Problem, that since Copernicus revived it, hath much exercised the Wits our best modern Astronomers and Philosophers, amongst which notwithstanding there hath not been any one who hath found out a certain manifestation either of the one or the other Doctrine.[2]"
References:
- Todd K. Timberlake, "Seeing Earth's Orbit in the Stars: Parallax and Aberration," arXiv Preprint Server, August 9, 2012.
- Robert Hooke, "An Attempt to Prove the Motion of the Earth by Observations."
Permanent Link to this article
Linked Keywords: Boy Scout; sixth grade; Boy Scouts of America; Boy Scouts of America membership controversies; fire; flint; steel; merit badge; vacuum tube; moss; north; tree; animal husbandry; reindeer; pacing; river; geometry; elementary school; similar triangle; geometer; Inkscape; algebra; triangle; high school; physics; guard railing; >Earth; trigonometry; ancient Greeks; Moon; parallax; Earth's rotation; diurnal parallax; fixed stars; celestial sphere; Todd Timberlake; Berry College (Mount Berry, Georgia); astrometry; arXiv Preprint Server; astronomer; geocentric model; universe; Copernicus; heliocentric system; Earth's orbit; scientist; instrumentation; century; Friedrich Bessel; Bessel functions; 61 Cygni; light year; milliarcsecond; stellar aberration; speed of light; meter per second; m/sec; orbital speed; speed of the Earth along its orbit; National Portrait Gallery, London; Ny Carlsberg Glyptotek; Wikimedia Commons; James Bradley; Astronomer Royal; arcseconds; Robert Hooke; gamma Draconis.